Filtro de dados e estimadores¶

1. Kalman
   1. Simbologia utilizada

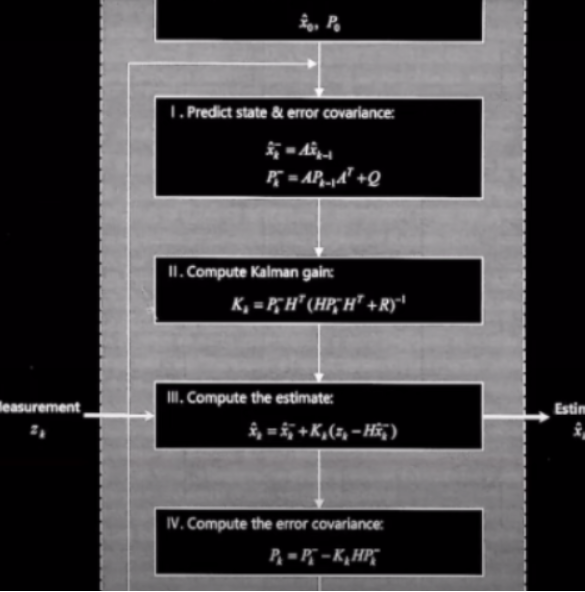
Na notação usual Zk é a k-ésima medição e ˆxk é a k-ésima estimativa. Perceba que a estimativa pode ser um estado diferente da medição, isto é, podemos por exemplo estar medindo a posição e estimando a velocidade, não precisam se tratar da mesma coisa, ai reside uma das vantagens inerentes ao filtro: ele não somente "filtra dados" ele também deriva variáveis não medidas a partir de um modelo (matriz A e Q). A princípio é difícil entender que diacho ta sendo expresso nesse diagrama. Vamos com calma, um passo de cada vez até o bendito Kalman. Temos no passo (I) uma etapa de predição (prediction), inclusive a notação embarca essa ideia, ˆx k- na notação usual é a previsão de estado k baseada na k-1, o "-" na notação quer dizer previsão, x antes de de fato termos a medição. Temos também Pk- é a covariância de erro prevista (medida de ruído/noise). Temos no passo (II) uma etapa é o estimation step.

1. Estimation Step

A principal etapa do estimation step é dada pela expressão:

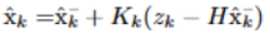
Aqui tomamos a previsão de xk (ˆxk-), a medição zk e obtemos a melhor estimativa ˆxk. Nesse passo usamos o Kalman gain (Kk) para ajustar a medida. Aqui para entendermos de de forma resumida o que é o Kalman gain, imagine uma média ponderada, isto é, cada medida tem um certo peso. O kalman gain é o peso associado a cada medição, ele é uma função que varia e atribui pesos maiores às medições que apresentam menor incerteza. A incerteza "a priori" (antes da medição) está de certo modo avaliadas na matriz Pk-(covariance square matriz). A matemática por traz desta matriz não é das mais triviais, não é absolutamente necessário entender por completo a matriz de covariâncias para aplicar o filtro, é possível consultar modelos já pronto de matrizes de covariâncias.

Já a matriz quadrada R é normalmente constante e depende das características dos sensores utilizados para realizar as medições. Cada elemento na matriz R representa a variância do ruído de medição para uma determinada observação, e os elementos fora da diagonal representam as covariâncias entre diferentes observações (se houver correlação entre os erros de medição).

São essas duas matrizes (Pk- e R) que utilizamos pra atualizar o Kk (kalman gain)

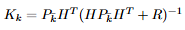
Tendo calculado o Kalman gain e sabendo Pk-, podemos atualizar calcular Pk (a posteriori). Essa matriz será fundamental no prediction step:

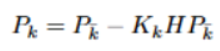
Perceba que a matriz H e R só aparecem no Estimation step. Antes que alguem reclame da matriz H, não se preocupem, no código exemplo vão perceber que é algo bem simples. Fundamentalmente, nem sempre o vetor Zk (medições) tem mesma dimensão que o vetor Xk (estimativss). Muitas vezes vamos estar prevendo variáveis que não estamos medindo,exemplo, medimos as posições e prevemos pelo filtro as velocidades também. A matriz H é a transformação linear que simplismente ajusta a dimensão dos vetores Xk. É uma matriz composta de 0's e 1's, simples assim :)

1. Prediction step

O prediction step é relativamente mais simples, é nele que vamos encontrar as variáveis "a priori". Aqui também entra a matriz A, que fundamentalmente contem as informações do modelo físico adotado. Se por exemplo estivermos analisando um movimento e supormos que se trata de um MRUV, é nessa matriz que isso ficará claro.

A primeira etapa desse passo é simples. Consiste em a partir da matriz A e de ˆxk- determinarmos ^xk. Isso se dá do seguinte modo:

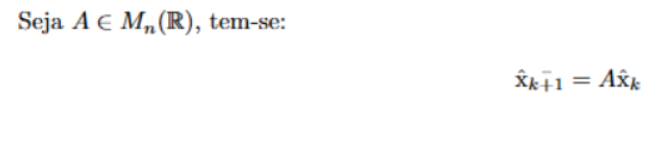
Um exemplo de matriz A seria o seguinte:

Vamos considerar um exemplo prático de aplicação do filtro de Kalman em um cenário de rastreamento de posição e velocidade de um objeto em movimento ao longo de uma dimensão (um problema comum em sistemas de navegação). Suponha que temos um objeto que se move com uma velocidade constante, mas estamos medindo apenas sua posição. Usaremos o filtro de Kalman para estimar tanto a posição quanto a velocidade. Têm-se:

Todos aqui sabem multiplicar matrizes, eu tenho certeza :) Pois bem, multiplique um 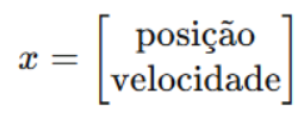à matriz A e veja o que acontece :)

A outra etapa desse passo é determinar a previsão da matriz de covariância, isto é, a matriz de covariancia "a priori".

Lembra que R representa a incerteza associada às medições? Pois bem, Q representa a incerteza associada ao modelo que adotamos.

Assim concluímos o prediction step e iniciamos novamente o estimation step, fazemos uma nova medição Zk. Os ciclos se repetem, assim a banda toca :)

1. Representação visual de como os passos se relacionam

Podemos representar visualmente o ciclo associado ao filtro:

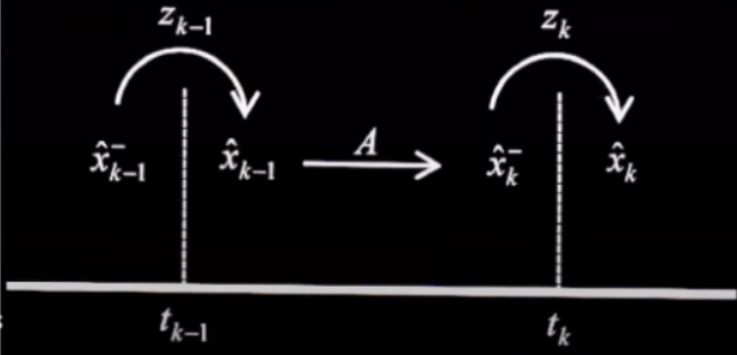
A princípio temos 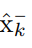, que é a previsão (k-1)-ésima (a priori). Introduzimos no sistema a medição Z(k-1) e a partir desta obtemos a (k-1)-ésima melhor estimativa de X. Esse foi o estimation step.
Aplicamos ao ^x(k-1) a matriz A e assim obtemos a k-ésima previsão de x. Este foi o prediction step. Novamente vamos aplicar o estimation step ... e assim por diante.

1. Código exemplo

Nos arquivos os senhores vão poder encontrar um arquivo de um código em matlab de um exemplo do filtro de kalman. Temos um móvel e medimos sua posição em x e y, supomos um MRUV. D Determinamos a melhor estimativa da posição (x,y) e da velocidade (x,y). No código introduzimos propositalmente ruídos gaussianos nas medições (o filtro lida melhor com esse tipo de ruído). Nos plots temos as posições medidas e as posições estimadas pelo filtro bem como as velocidades estimadas pelo filtro